2023.02.19 - [Computer Science/Matlab(수학)] - 매트랩 [2계 상미분방정식] 라플라스 변환 (Laplace Transform)
매트랩 [2계 상미분방정식] 라플라스 변환 (Laplace Transform)
Laplace 변환은 공학자들에게 기본적으로 중요하다. 상미분방정식의 풀이 과정을 대수적 문제의 풀이 과정으로 단순화 한다는 장점이 있다. Laplace 변환의 공식은 Laplace 변환의 장점은 첫째, 상미
greedy-engineer.tistory.com
기본적인 라플라스 변환으로 상미분방정식을 푸는 풀이가 궁금하다면 위에 게시물을 참고하자.
2계 상미분방정식 중 구동력이 불연속적인 문제를 풀어보자. 문제는 감쇠 용수철 운동으로 구동력이 범위 0~pi에서 sin 함수인 방정식이다.
방정식은 아래와 같다.
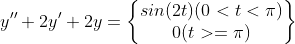
구동력이 t 의 범위에 따라 달라지는 함수를 단위 계단 함수 (Unit Step Function or Heaviside Function)이라고 하고 매트랩에서 지원해 주는 표현 방식으로 heaviside(t) - heaviside(t-pi) 라고 표현 가능하다.
매트랩을 이용한 풀이를 진행해 보자!
1. 상미분 방정식 설정
% set equation
syms y(t) Y_LT s % Y_LT 는 y의 라플라스 변환이다. (미리 설정)
ode = diff(y,t,2) + 2*diff(y) + 2*y == (heaviside(t) - heaviside(t-pi))*10*sin(2*t);heaviside(t) - heaviside(t-pi)의 이해를 돕기 위해 따로 그래프를 하나 그리면,

여기에 sin(2t)를 곱한다.
2. 초기 조건 설정
% initial conditions
Dy = diff(y);
conds = [laplace(y(t), t, s) y(0) Dy];
values = [Y_LT 1 -5];매트랩 함수 'subs'를 이용하여 라플라스 변환된 방정식에서 conds 안에 세 개의 값과 values 안에 세 개의 값을 바꾸기 위해서 미리 설정해 준다.
3. 라플라스 변환. 방정식 풀이
ode_LT = laplace(ode);
ode_LT = subs(ode_LT, conds, values);
Y_LT = solve(ode_LT, Y_LT);
Y_LT = ilaplace(Y_LT);
% simplifies ilaplace in Y_LT. Without this, cannot plot
Y_LT=simplify(Y_LT);기본적인 라플라스 변환 풀이법은 위에 언급한 게시물에 나와있으니 참고!
'fplot'로 그래프를 그리기 위해, 'simplify'를 이용해서 방정식을 단순화시킨다.
4. 그래프 그리기
hold on
fplot(Y_LT, [0 5*pi])
hold off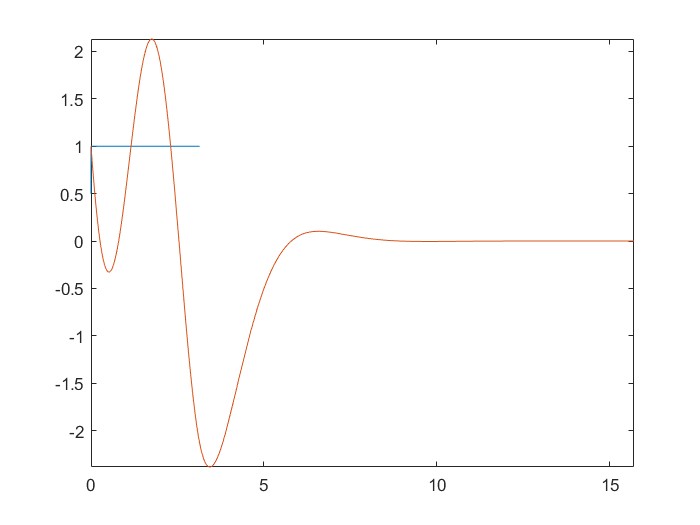
간단하게 감쇠 용수철 운동을 라플라스 변환을 통해 풀어봤다!
'Computer Science > Matlab(수학)' 카테고리의 다른 글
| 매트랩 [선형 대수] 행렬(matrix), 사다리꼴 행렬(row echelon form), 행렬식(determinant) (0) | 2023.03.05 |
|---|---|
| 매트랩 [2계 상미분방정식] 라플라스 변환과 합성곱 (Laplace Transform and Convolution) (0) | 2023.03.05 |
| 매트랩 [2계 상미분방정식] 라플라스 변환 (Laplace Transform) (0) | 2023.02.19 |
| 매트랩 [2계 상미분방정식]의 연립 방정식으로의 변환 (수치적, 해석적 풀이) (0) | 2023.02.16 |
| 매트랩 [2계 상미분방정식] 초기값 문제. 용수철 운동 그래프 그리기. (0) | 2023.02.08 |
